Using SAS to test whether “It gets better” makes you gay

Next question on categorical data analysis …
Correlated proportions. There are a lot of reasons why you might have correlated data in a two-way contingency table. The most common is that you have measured people twice.
I have heard people say that including discussion of homosexuality in school makes it more likely that children would become gay. Personally, I think, this is – and this is a technical term here – total bullshit.
If I were to test this hypothesis, I could survey a group of 141 male students and ask them several questions, including,
“Would you consider having sex with Bob?”
I would include the picture of Bob above so we are clear what we are talking about here and there is no misunderstanding that I really meant to say Bobbette or Bobbi or Bobby Lou.
Six months later, after having read about people like Alan Turing , the same students would take the same survey. I do not have 282 students here, I have 141 students tested twice.
Some people might say the only satisfactory outcome shows at a minimum all of the students who previously stated that Bob was not their type still saying, “No”. Even better would be if some of those who previously said they would consider it now are in the anti-Bob category.
In fact, we instead get something like shown in the output below, with 1 of the students who said no previously now saying “Yes” and one of those who previously said, “Yes” now being on a no-Bob diet.
Having taught adolescents, I suspect that our two who changed boxes either were not paying attention the first time, were being a smart-ass by checking “Yes”, or were too timid to admit that Bob is indeed their cup of tea.
Statistically speaking, my hypothesis is that learning about famous people who were homosexual and learning about intolerance and discrimination against homosexuals does not make one gay. My null hypothesis is that there is zero difference between time one and time two. Another hypothesis I could test is that the level of agreement in Bob-attraction is 1.0 between time1 and time2.
To test both of these hypotheses using SAS all I need to do is this:
TITLE "MCNEMAR AND KAPPA WITH COMPLETELY FABRICATED DATA" ;
PROC FREQ DATA = AREYOUGAY ;
TABLES BOB*BOB2 / AGREE ;
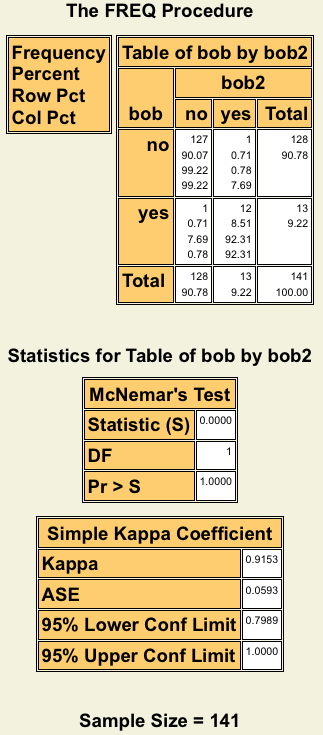
Using my completely made up data, you can see that the value of McNemar’s Test is 0 and the probability of a greater S = 1.00 . This being a very far cry from .05, we accept the null hypothesis that there is no difference between the proportion of male students who are gay (or, at least interested in guys like Bob) pre- and post class discussions of historical contributions and issues of gay people.
In the next table, we see that the Kappa coefficient is .9153 and that 1.00 is within the 95% confidence interval, so we can conclude it is plausible that there is perfect agreement. Of course, one could point out that .79 is also a plausible value, so maybe those classes did make one student gay after all. I would counter with, but I already accepted the null hypothesis of no difference based on the McNemar test, so there!
There you have it, two statistical tests to decide if the “It gets better” movement and classes on gay history make you gay.
Please note, since we want to be correct here (statistically, not politically) that McNemar is only used for two by two tables. If you had multiple options like,
“Yes”, “Only if he looks like a real man under that damn My Little Pony costume.” and “No” then you would not use McNemar. You would use Cochran’s Q. That, however, is a post for some other day. My next post, in case you are dying to know, is on survival analysis in pictures.
Mcnemar’s test is really a quite misleading statistic. It only measures lack of symmetry not disagreement. Its possible to have 100% disagreement and a mcnemar of 0.
R
I use McNemar’s test quite often. It’s a great tool for quick answers to consulting questions.
It’s also possible to have significant agreement in Kappa *and* significant (non-symmetric) disagreement in McNemar’s test. Agreement and Disagreement are not mutually exclusive.
My brother passed away and this guy looks just like him can anyone tell me his name ?!?