Categorical Data & Bivariate Descriptive Statistics

The Agresti and Finlay book,  Statistical methods in the social sciences , has a nice section on bivariate descriptive statistics.  (And thank you to the person on twitter who recommended that book. I apologize that I can’t remember who it was.) I got to thinking about that today, especially with regard to categorical data. Often when working with categorical data our interest is in predicting which category a person falls into. Will you vote for Obama next November, for whoever the Republicans nominate, a third-party candidate or just stay home? Will you buy my fabulous widget or just click on to the next page?

I’m interested in something else with descriptive statistics today. Say I already know what category you are in, what does that tell me? The answer is maybe a lot and maybe nothing.

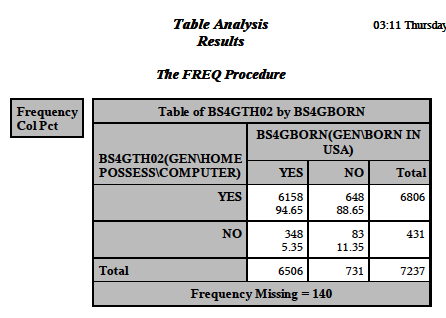
Let’s take two examples.The first uses two categorical variables, do you have a computer at home and were you born in the U.S. All respondents were eighth-grade students who were part of the 2007 Trends in International Mathematics and Science Study (TIMSS) .

The table above shows the frequency for each cell, e.g. how many said  YES or NO to Have a home computer & YES or NO to Born in the US. It also shows the percentage of the column giving one response or the other. So, 94.65% of those born in the U.S. have a computer at home versus 88.65% of those not born in the U.S. Out of our total 7,237 responses only 431 students said they did not have a computer at home. This was 5% of those who were born in the U.S. and 11% of those who were not.  As a teacher, can this information help me? Maybe? Here is what I can conclude

1. The great majority of students have a home computer, almost nine out of ten students who were not born in the U.S. do and more than 9 out of 10 of those who were born here.
2. Assuming your class is a mix of students who are and are not native born, which describes most classes in California, it is a good bet that over 90% of your students have a computer at home. (The average for the total sample was over 94%.)
3. If you know that a student was not born in the U.S., you know that he or she is twice as likely as U.S. born students to not have a computer at home (11% versus 5%) but on the other hand you also know that the odds are about 8 to 1 that the student does have a computer.

Does any of that do you any good? Maybe. Why not just ask the students if they have access to a computer? You could do that certainly. Some teachers feel uncomfortable asking questions like that because they feel like it is intrusive or it might make students feel uncomfortable if they are the only kid in the class who doesn’t have a computer. I think the information does some good because teachers often assume that students in low-income families or from immigrant families don’t have computers, email or Internet access and thus don’t assign homework that uses these resources. The data show that assumption is usually incorrect. If more than one out of ten students who are not born in this country do not have access to a home computer and I was working with a class of primarily immigrant children, I would certainly take that into account in my planning.

What other statistics would I like to have at this point? What other analyses might I do? There are several that spring to mind right away:

• I could re-run that table analysis to show row percentages and total percentages. I didn’t do it that way because I thought it was easier to read and it isn’t a big deal for me to estimate the other percentages, but other readers might prefer to have the percentages given.
• Since plenty of children are born in the U.S. to immigrant parents, it might be more useful to re-run this analysis looking at if the parent was born in the U.S. That may be more strongly correlated with socioeconomic factors than the child’s birthplace. Or maybe not, because the child’s birthplace undoubtedly relates to how long you’ve lived in this country – at least 13 years if your 13-year-old was born here.
• Speaking of SES, it might be more useful to use information like the family income or parent’s education instead of or in addition to where the parent or child was born.
• What else can we know about students who don’t have a computer at home? What else might that not have? Is this a proxy for having limited academic support materials in the home like books, a calculator, etc.?

The second uses the graphs I produced with SAS On-Demand to look at a categorical variable – do you have a computer at home – and an ordinal variable – the number of books you own. This is where I said MAYBE knowing the child does not have computer at home will tell you nothing. If both of these distributions were the same, that would be the case (at least as far as books) but both distributions are not the same.

Curiously, knowing that the child has a computer tells you very little. Why is that?  Let’s look at the distribution.

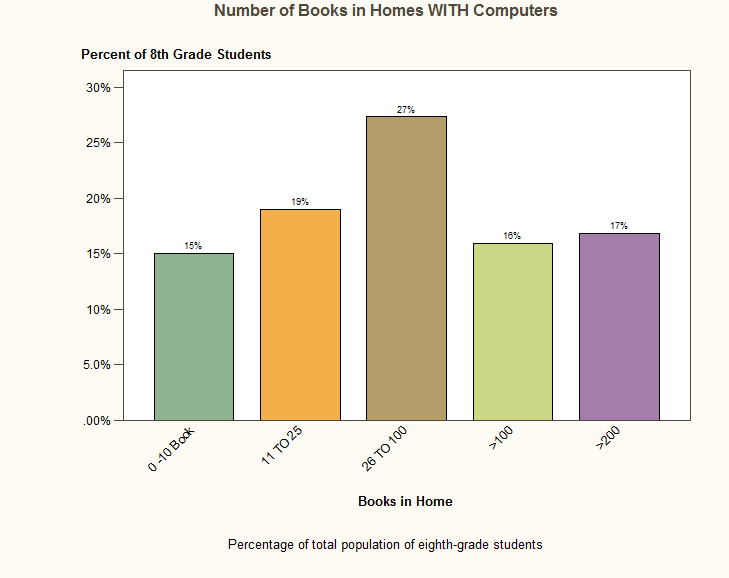Out of the total population, 94% of students have a computer and the median for those computer owners is 26-100 books in the home. They are almost exactly equally likely (34% vs 33%) to have less than that or more than that. So a child who has a computer is like the vast majority of the population and for that population access to books at home is all over the map.

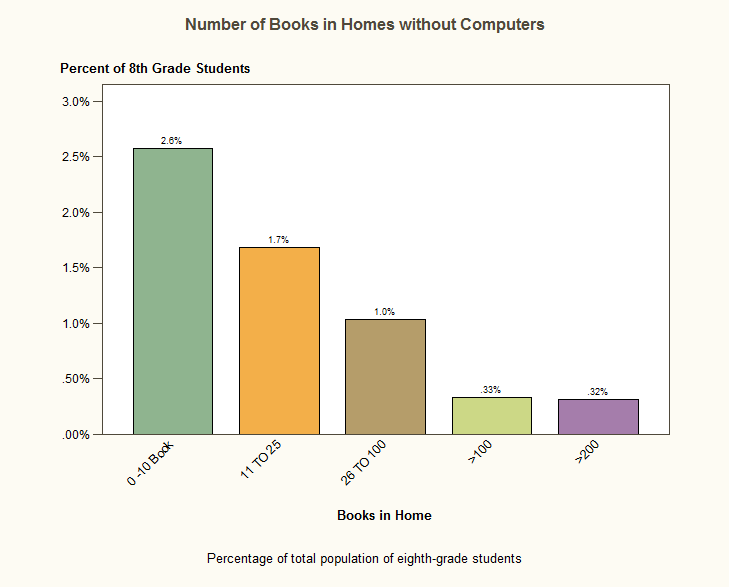
Now let’s look at whether a child does NOT have a home computer.

This is about 6% of the population. The median number of books for those children is 11-25, so it is less than the typical student. It is also a very skewed distribution. Children without a home computer are much more likely to have FEWER than 11 books than to have more. If we look back and forth between the two graphs, we can see that a child with a home computer has about a 1 in 6 chance of having more than 200 books at home. A child without a home computer has about a 1 in 20 chance of having more than 200 books at home.

As a teacher, if I knew that several of my students didn’t have a computer at home, I’d have a fair degree of certainty that they did not have a lot of books at home either (a lot being defined as 100 or more).

I find examples like this one interesting because at first glance, it doesn’t seem possible that knowing a student DOES have a computer tells you very little while knowing that he/she DOES NOT have a computer can provide you useful information.

Which just goes to show you that you should always take a second glance.

 

P.S. If I were that teacher, I would make a major effort to introduce my students to the public library – organize a field trip, invite a librarian to visit.