SAS and SPSS Give Different Results for Logistic Regression but not really

When people ask me what type of statistical software to use, I run through the advantages and disadvantages, but always conclude,

“Of course, whatever you choose is going to give you the same results. It’s not as if you’re going to get a F-value of 67.24 with SAS and one of 2.08 with Stata. Your results are still going to be significant, or not, the explained variance is going to be the same.”

There are actually a few cases where you will get different results and last week I ran across one of them.

A semi-true story

While I was under the influence of alcohol/ drugs that caused me to hallucinate about having spare time during the current decade, I agreed to give a workshop on categorical data analysis at the WUSS conference this fall . After I sobered up (don’t you know, all of my saddest stories begin this way), I realized it would be a heck of a lot easier to use data I already had lying around than go to any actual, you know, effort.

I had run a logistic regression with SPSS with the dependent variable of marriage (0 = no, 1 = yes) and independent variable of career choice (computer science or French literature ). There were no problems with missing data, sample size, quasi-complete separation, because like all data that has no quality issues, I had just completely made it up. I thought I would just re-use the same dataset for my SAS class.

So, here we have the SPSS syntax

LOGISTIC REGRESSION VARIABLES Married

/METHOD=ENTER Career

/CONTRAST (Career)=Indicator

/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

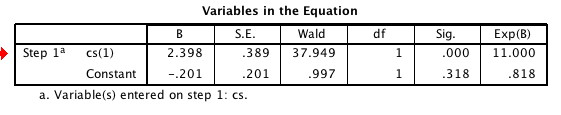As I went on at great boring length in another post, if you take e to the parameter estimate B, (  Exp(B) in other words) you get the odds ratio for computer scientists getting married versus French literature majors, which are 11 to 1.

Also, I don’t show it here but you can just take my word for it,

the Cox & Snell R-square was .220 and the Nagelkerke R-square was .306 .

If you are familiar with Analysis of Variance and multiple regression, you can think of these as two different approximations of the R-squared and read more about pseudo R-squared values on the UCLA Academic Technology Services page.

So, I run the same analysis with SAS, same data set and again, I just accept whatever the default is for the program.
proc logistic data = in.marriage    ;
class cs  ;
model married = cs /   expb  rsquare;

If you look at the results, you see there is an

R-squared value of .220 and something called a Max-rescaled R-squared of .306

Okay, so far so good, but what is this?

For our parameter estimate for both the intercept and our predictor variable we get completely different values,  and, in fact, the relationship with career choice is  NEGATIVE but the Wald chi-square and significance level for the independent variable, is exactly the same. (This is what we care about most.)

The odds ratio is different, but wait, isn’t this just the inverse? That is .091 is 1 /11  so SAS is just saying we have 1:11 odds instead of 11:1

Difference number 1: SAS uses the lower value as the reference group, for example NOT being married.

That’s easy to fix. I do this:

Title "Logistic - Default Descending" ;
proc logistic data = in.marriage descending   ;
class cs  ;
model married = cs /   expb  rsquare;

This is a little better, The two R-squared values are still the same, the odds ratio is now the same, at least the relationship between the CS variable and marriage is now positive. You can see the results here or the most relevant table is pasted below if you are too lazy to click or you have no arms (in which case, sorry for my insensitivity about that and if you lost your arms in the war, thank you for your service <– Unlike everything else in this blog, I meant that.)

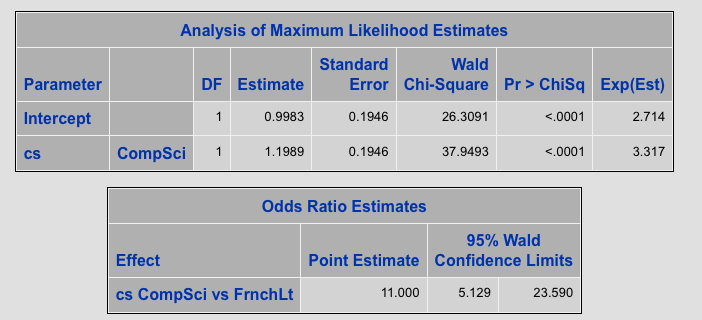BUT, the parameter values are still not the same as what you get from SPSS and Exp(B) still does not equal the odds ratio.

Since actual work is calling me, I will give you the punch line thanks very much to David Schlotzhauer of SAS,

“If the predictor variable in question is specified in the CLASS statement with no options, then the odds ratio estimate is not computed by simply exponentiating the parameter estimate as discussed in this usage note:

http://support.sas.com/kb/23087

If you use the PARAM=REF option in the CLASS statement to use reference parameterization rather than the default effects parameterization, then the odds ratio estimate is obtained by exponentiating the parameter estimate.  For either parameterization the correct estimates are automatically provided in the Odds Ratio Estimates table produced by PROC LOGISTIC for any variable not involved in interactions.”

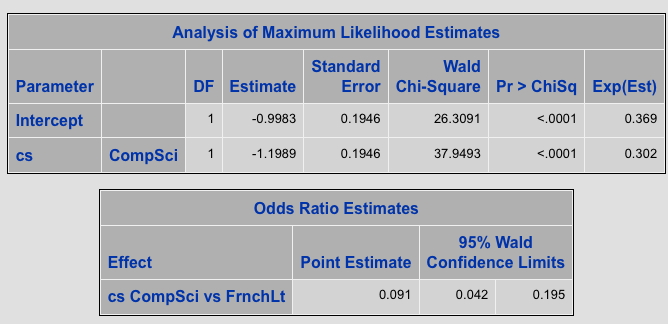
So, the SAS code to get the exact same results as SPSS is this (notice the PARAM = ref option on the class statement)

Title “Logistic Param = REF” ;
proc logistic data = in.marriage descending   ;
class cs/ param = ref ;
model married = cs /   expb  rsquare;

You can see the output here.

Did you notice that the estimate with the PARAM = REF (the same estimate as SPSS  produces by default)  is exactly double the estimate you get by default with the DESCENDING option? That can’t be a coincidence, can it?

If you want to know why, read the section on odds ratios in the SAS/STAT User Guide section on the LOGISTIC Procedure. You’ll find your answer at the bottom of page 3,952  (<— I did not make that up. It’s really on page 3,952 ).