The Facts of Factor Patterns
About a week ago, I went through pointing and clicking your way to a factor analysis. At the time, I suggested rotating the factors. Now we’re going to interpret the rotated factor pattern. Let me recap, briefly. Agresti and Finlay (p.532) put it way better than me when they said:
Factor analysis is a multivariate statistical technique used for …
1. Revealing patterns of interrelationships among variables
2. Detecting clusters of variables, each of which contains variables that are strongly intercorrelated …
3. Reducing a large number of variables to a smaller number of statistically uncorrelated variables, the factors of factor analysis.
All of which is well and good but once you have your factors, what do they mean? How do you interpret them?
Important point one: The correlation of a variable with a factor is called the loading.
Important point two: To ease interpretation we’d really like to have “simple structure”, that is, where variables load close to 1.0 on one factor and close to zero on the others. I mean, really, if you think about it, if your items load equally on all factors it’s going to be pretty hard to interpret.
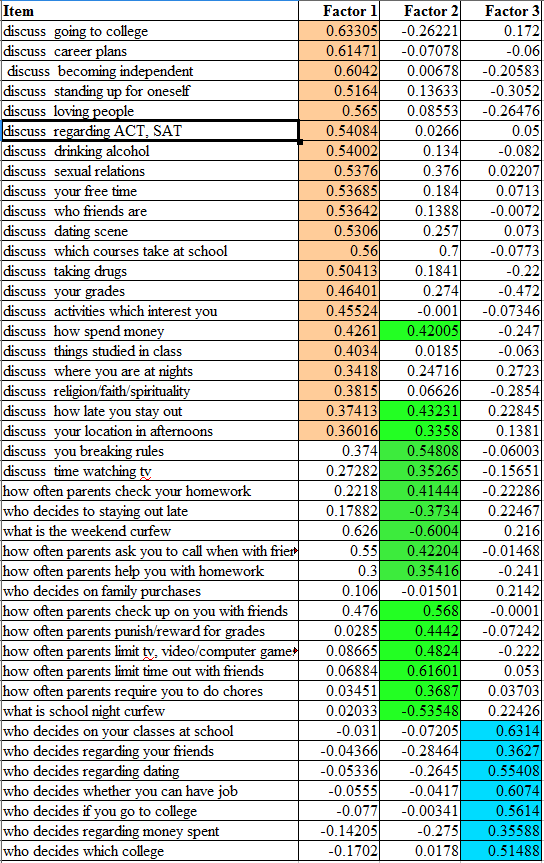
Let’s take a look at my example from the 500 Family Study, which you have probably forgotten already. To make it easier to interpret, I copied the factor pattern output into a spreadsheet and sorted by the loadings on the first, second and third factor. You can see that almost all of the items relating to discussion loaded on the first factor. So, I could say that factor 1 is “Communication with parents”. The second factor seems to be mostly about rules, punishment and placing limits, such as punishments or reward for grades, curfew and time out with friends. The discussion questions that load more on this factor than the first are on discussion of breaking rules and discussion of curfew. The third factor is all of the items related to decision-making, with the exception of family purchases, which didn’t really load on any of the three factors.
Notice a few things— Just like correlations, loadings can be positive or negative. How late your curfew is loads negatively on the Rules Factor. That is, families that have stricter rules have an earlier curfew. How often parents limit time out with your friends loads positively on the Rules Factor. Although it’s not ideal, variables can load on more than one factor. As noted, the discussion of breaking rules item loads both on the Communication Factor and the Rules Factor. Variables can not load on any factor at all, like the decision on family purchases. My guess is that most parents decide most purchases without consulting their adolescent children.
The really useful result of factor analysis is that it allows you to take your 42 items, discard one as not really fitting and distill the others down into three factors. Instead of using 41 individual items to predict your outcome of interest, say delinquent behavior, you can use three. It’s almost certain that those three factors will be far more reliable than any individual item, and your results will be far easier to explain as well, say, “Students who have more communication with their parents, moderate rules and moderate input on decision-making have the lowest rate of delinquent behavior and highest academic achievement.”
Not sure if that is true or not but with these factors we are now in a good position to test that. I just need a couple more measures, of delinquent behavior and academic achievement, and I can test my hypotheses. I expect there will be a linear relationship with communication (negative for delinquency and positive for academics) and a curvilinear relationship with the other two measures (inverse for delinquency).
I guess that will be my next thing to do when I have some spare time. Or, you can wander on over to ICPSR.org and download the 500 Family Study data yourself.