Today, I was thinking about residuals & maybe Heisenberg

I’m working on the SAS Naked Mole Rat book and was writing about residual variance. It occurred to me that I just threw in a chart and assumed that people would know what residual variance was and moved right along. This reminds me of the  time the rocket scientist had a sign outside of his office that said,

“Heisenberg may have slept here.”

He was surprised that no one laughed. He said,

“I’d think everyone would have heard of the Heisenberg Uncertainty Principle.”

Uh, no

Below you can see where I plotted the residuals the predictor (pretest score) for a dichotomous variable, passed course, coded as yes or no.

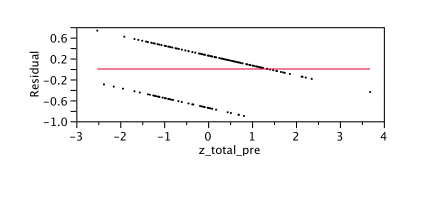Nice graph. What does it mean, exactly?  Let’s start with what residual is. The residual is the actual (observed) value minus the predicted value. If you have a negative value for a residual it means the actual value was LESS than the predicted value.  The person actually did worse than you predicted. If you have a positive value for residual, it means the actual value was MORE than the predicted value. The person actually did better than you predicted. Got that?

It’s worth belaboring this point because I think it is a bit counter-intuitive. Or maybe it’s just me. So, look at the line above, which is at zero. If there is a residual error of zero it means your prediction was exactly correct. Under the line, you OVER-predicted, so you have a negative residual. Above the line, you UNDER-predicted, so you have a positive residual. Naw, it isn’t just me. That really is counter-intuitive, but that’s the way it is. (Ryan Rosario, on twitter, source of all knowledge second only to wikipedia (twitter in general, that is, not Ryan specifically, although he does seem to be pretty smart), pointed out that one way of thinking of it is that a positive residual error means your actual result is OVER the predicted one, that you OVER-achieved. So, it may make sense in a twisted way.)

Back to the graph  – the x-axis is labeled “z_total_pre”. It is the z-score for the total on the pre-test. As you might remember from your first statistics course, a z-score is a standardized score where a 0 is the mean and 1 is the standard deviation. So, a person with a z-score of 0 is exactly average, a negative z-score is below average and a positive z-score is above average. Assuming a normal distribution, a person with a z-score of +1.0 scores above 84% of the population, that is, in the top 16%. A person with a z-score of -1.0 is in the bottom 16%. A person with a z-score of +2.0 is in the top 2.5% and with a -2.0 z-score in the bottom 2.5%.

If you have an unbiased predictor, you should be equally likely to predict too high or too low. The mean of your error should be zero. It should also be zero at all points. No one is going to be too happy if you say that your predictor isn’t very good for “A” students. However, it seems that is exactly what’s happening. In fact, past about 1.5 standard deviations above the mean, ALL of our students have been over-predicted. Let’s look at our graph again. I have helpfully pasted it below again so that you don’t have to  scroll all the way back. That would be annoying. Besides, I get paid by the page.

We have two students who scored very low on the pretest, around -2.5 standard deviations. We used their pre-test scores to predict whether the student would pass or fail. One of them had an actual score on the greater than predicted – a residual of about .65 , the other had an actual score less than the predicted, with residual error around -.2 .

As you can see, past a z-score of about 1.5 all of the residual values are negative. That means that for the top 10% or so of the students, we had an actual value that was less than the predicted value. So, this is NOT an unbiased predictor. It is biased in favor of the high-scoring students. I am bound by the Statistician’s Code to consider bias bad.

Let’s think about residual error in a hypothetical situation. Let’s say we have prediction for males and females and that the females tend to have their performance over-predicted (just like the high scorers in our example above). Let’s say that based on your score, you, a male, were denied admission to the program. Could you argue, based on statistical evidence, that the selection test was biased in favor of women. Why, yes, you could.

There are other things I could say about residuals, but the rocket scientist just came home, bearing groceries and a bottle of wine. Maybe I will go drink Chardonnay and talk to him about Heisenberg.