We NEED statistics because you don’t know it when you see it

When we started the Dakota Learning Project to evaluate our educational games, I wondered if we had bitten off more than we could chew. We proposed to develop the games, pilot them in schools, collect data and analyze the data to see if the games had any impact. We were also going to go back and revise the games based on feedback from the students and teachers.

Some people told us this was far too much and we should just do a qualitative study observing the students playing the game and having them “think aloud”. Another competition we applied to for funding turned us down and one of the reasons they gave is that we were proposing too much.

We ended up doing a mixed methods design, collecting both qualitative and quantitative data and I’m very glad I did not listen to any of these people telling me that it was too much.

There is no substitute for statistics.

When I observed the students in the labs, I thought that perhaps the grade level assigned to specific problems was inconsistent with what the students could really do. For example:

Add and subtract within 1000 … is at the second-grade level 

Multiply one-digit numbers  … is at the third-grade level

It seemed to me that students were having a harder time with the supposedly second-grade problem, but I wasn’t sure if that was really true. Maybe I was seeing the same students miss it over and over. After all, we had 591 students play Spirit Lake in this round of beta testing. It was certainly possible I saw the same students more than once. It is definitely the case that students who were frustrated and just could not get a problem stuck in my mind.

So …. I went back to the data. These data do double-duty because  I’m teaching a statistics class this fall and I am a HUGE advocate of graduate students getting their hands on real data, and here was some actual real data to hand them. (I always analyze the data in advance so it is easy to grade the students’ papers, to give examples in class and so l don’t get student complaining that I am trying to get them to do my work for me, although they still do. Ha! As if.)

We had 1,940 problems answered so, obviously, students answered more than one problem each.  Of those problems, 1,053, or 54.3% were answered on the first attempt. This made me quite happy because it is close to an ideal item difficulty level. Too easy and students get bored. Too hard and they get frustrated.

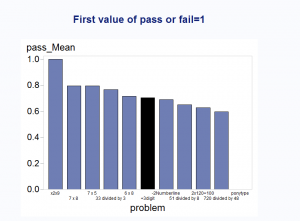
I used SAS Enterprise guide to produce the chart below:

You can see that the subtraction problem showed up about mid-range in difficulty. Now, it should be noted that the group gets more selective as you move along. That is, you don’t get to the multiplication problems unless you passed the subtraction problem. Still, it is worth noting that only 70% of fourth- and fifth-grade students in our sample answered correctly on the first try a problem that was supposedly a second-grade question.

Because we want students to start the game succeeding, I added a simpler problem at the beginning. That’s the first bar with 100% of the students answering it correctly. I won’t get too excited about that yet, as I added it later in the study and only a few students were presented that problem. Still, it looks promising.

So, what did I learn that I couldn’t learn without statistics? Well, it reinforced my intuition that the subtraction problem was harder than the multiplication ones and told me that  a substantial proportion of students were failing it on the first try. It was not the same students failing over and over.

The second question then, was whether the instructional materials made any difference. I’m pleased to tell you that they did. On the second (or higher) attempt, 85% of the students answered correctly. If you add the .85 of the 30% who failed the first go-round to the 70% who passed on the first attempt, you get 92% of the students continuing on in the game. This made me happy because it shows that we are beginning at an appropriate level of difficulty. I would have liked 100% but you can’t have everything.

I should note that the questions are NOT multiple choice, and in fact, the answer to that particular problem is 599, so it is not likely the student would have just guessed it on the second attempt.