Computers, public libraries and beware the cell chi-square
When the first computer lab was put into the tribal college where I was a consultant, the professor in charge of the project complained that students were spending time in the lab on Yahoo, MySpace, emailing friends on other reservations, downloading software and all sorts of non-academic activities. He asked what he should do. I answered, “Let them, and count your blessings.”
That experience is consistent with the research showing that Native Americans make greater use of public internet facilities – principally school computer labs and library computers – than does the population at large.
Experiences like that one explain why I am a huge fan of public libraries. The rise of computers use for school work, wikipedia replacing the encyclopedia has made me even a bigger advocate. I have always believed that kids who don’t have computers at home, by necessity, make more use of library computers – but can I prove it?
Since I had my hands on the 2007 Trends in International Mathematics and Science Study (TIMSS) data, I thought I’d take a look at the relationship between having a computer at home and use of a computer elsewhere. The nice thing about the TIMSS data is it specifically asked about school computer use, so the questions asked were:
Do you use a computer at home?
Do you use a computer at school?
Do you use a computer elswhere (public library, internet cafe, friend’s house)?
It is true that this last question does combine a number of options (although I don’t think too many eighth-graders are going to Internet cafes). That’s what happens when you use data you didn’t collect yourself, but I decided to plow ahead anyway….
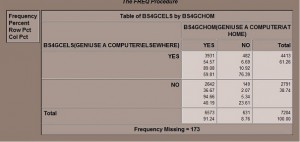
Below is the cross-tabulation of Use of computer at home by Use of computer elsewhere.
A couple of points I noted are:
- 91% of students in the survey DO use a computer at home
- Most students use a computer elsewhere whether they have a computer at home or not
- More students who DON’T have a computer at home (76%) use a computer other places, like at the library, than students who DO have a computer (60%)
- Another way to look at this is that students who DON’T have a computer at home are three times as likely to use a computer elsewhere as not about 75- 25. For students who DO have a computer at home, the odds are 60-40.
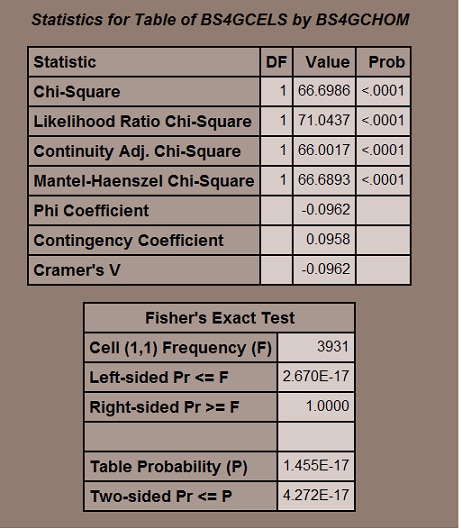
So, given all of this, it seems like for that 9% of students who don’t have a computer at home, access to computers other places is relatively more important. Let’s look at this in terms of statistical significance. We can start by looking at a chi-square value, shown below.
So, we have a fairly whopping chi-square of over 66 with a p-value less than .0001 . This tells us that that there is a very significant relationship between having a computer at home (or not) and using a computer somewhere else. The Fisher’s exact test similarly rejects the null hypothesis. So, there is a relationship.
But that doesn’t really answer the question. The specific question I want answered is do students who don’t have a computer at home use computers elsewhere more than students who do.
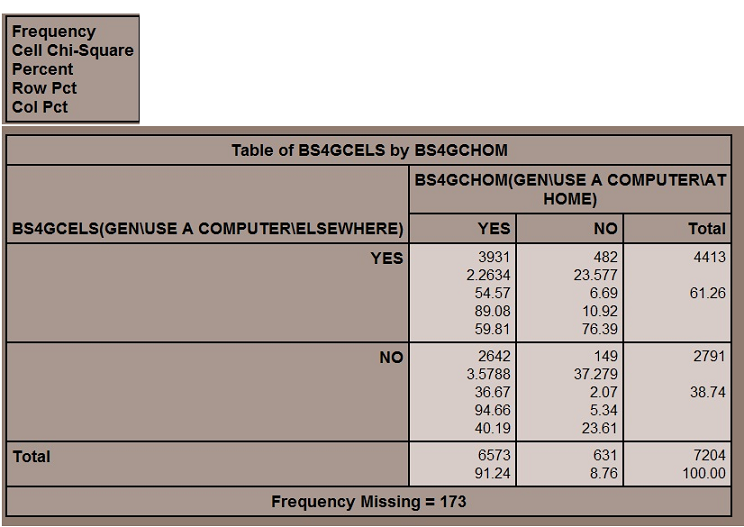
In this case, do I want to look at the cell chi-square value. That is, how much does each individual cell contribute to the overall relationship? Out of the chi-square value of 66, about 60 of it is due to the two cells under students who do NOT have a computer at home.
So does this tell me that I am right because the cell chi-square values for those in the “Do not have computer at home” column are so large?
Yes, and no, not at all. Yes, I am right. There is a relationship between not having a computer at home and using computers elsewhere more. The significant chi-square tells me that and the much higher odds of students who don’t have a home computer using one elsewhere tells me that also.
The cell chi-square does NOT tell me that. In fact, a cell chi-square value is comparing the obtained distribution between the cells to the expected distribution based on the population. In a case like this, where you have over 91% of the population in one column, the expectation is going to be driven by that 91%.
About 61% of the population uses computers outside home and school. If there is no relationship between having a computer at home and use of a computer elsewhere, you would find about 61% of the people using a computer elsewhere – for the population who have a computer at home, the figure is 60% (okay, 59.8%). But wait a minute! That 61% was based on a population comprised overwhelmingly of that group, people with computers at home.
What if we took a stratified random sample where we had equal samples of students with and without computers at home? Would our cell chi-square values be about the same for the two groups? Yes, yes, they would. Check back tomorrow for proof.
This doesn’t mean cell chi-square values are useless or should not be intepreted, by the way. It just means that in some cases where you have a very unequal distribution, you can be misled if you are not careful.
The code for doing these analyses is below, by the way. The first statement creates the Html page and uses the brown style, because I like brown.
The second statement invokes the SAS FREQ procedure.
The first TABLES statement just does the cross-tabulation between the two variables for using computers elsewhere and at home.
The second TABLES statement does a cross-tabulation of the variable for using computers elsewhere ( BS4GCELS) with using computers at home (BS4GCHOM) and at school ( BS4GCSch) . The options at the end of that statement request a chi-square and cell chi-square.
ods html file = "C:\TIMSS\sasout\chisq.html" style = brown ;
proc freq data = lib.student_int ;
tables Bs4GCels* BS4GCHOM ;
tables BS4GCELS* (BS4GCHOM BS4GCSch) / chisq cellchi2 ;
run ;
ods html close ;