The F-statistic in ANOVA explained
I tried to find an easily comprehended explanation of the F-statistic for my students but I could not, so, here as a public service is mine. If you have some other pages you can recommend, please let me know.
Okay, why ANOVA? Why not just do a t-test? Well, let’s say you have five groups. Then you will have ten pairwise comparisons. You compare group 1 to groups 2, 3, 4 and 5. That’s four. Now you compare group 2 to groups 3, 4 and 5. That’s another three t-tests. And so on. So now, you don’t really have a 5% probability of a type I error when p = .05 because you actually had TEN tests. If you did 100 tests, you’d expect five of them to turn out significant just by chance. So, let’s just accept that many pairwise tests = bad.
Enter ANOVA, short for Analysis of Variance. Let’s talk about a one-way ANOVA for now. You have a continuous, numeric dependent variable – say height. You have a categorical independent variable with two or more levels. You could do ANOVA with just two levels but in that case you might as well do a t-test. In this case, let’s assume that we have children raised eating an unrestricted diet, children who were raised vegetarian and children who were raised vegan. At age 10, we decide to measure all of their heights.
What is our null hypothesis? It is that there is no difference among the means, or
μ1 = μ2 = μ3
Enter the F-test. We are going to state that if there is no difference in the means then the estimate of variance you get from the difference in group means should be the same as the estimate of the population variance you get within groups. The F statistic is calculated like this
variance between groups
variance within groups
If the null hypothesis is correct, these two estimates of the variance should be close to the same and your F ratio should be near 1.0
How to get the within group variance
Well, it’s just like any other time you get a variance. Imagine that group 1 is a sample for a study. What do you do? You sum the squared deviations for the mean and divide by n minus 1, right?
That gives you the within group variance for group 1. You do the same thing for group 2 and group 3.
BUT … not all groups are created equal. What if you have five times as many people in group 3 as you do in group1 and group 2?
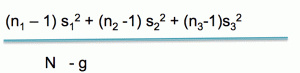 Being the reasonable person you are, you weight the within group variances by the degrees of freedom of each group, that is to say, the number of subjects minus 1. You divide this by the total number of subjects minus the number of groups. This is your within group estimate of the variance. This is your denominator. Let’s say that the value you get for this is 42.
Being the reasonable person you are, you weight the within group variances by the degrees of freedom of each group, that is to say, the number of subjects minus 1. You divide this by the total number of subjects minus the number of groups. This is your within group estimate of the variance. This is your denominator. Let’s say that the value you get for this is 42.
Now you need the between groups variance
First, subtract each group mean from the overall mean. Square that.
Second, multiply by the number in each group
Third, add the result
Fourth, divide by the number of groups minus 1
Let’s just suppose, for the sake of supposing, that the value you get for this is 108. Your F-ratio is then 108/42 = 2.57
And that, my dears is you get an F value.
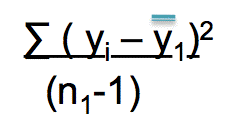
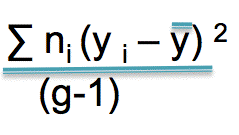
Great Blog Annmaria. This post wold be much better with nice equations (check http://www.mathjax.org/, I use it and it is free and easy))
Thanks a lot. I’ve been looking for something like that because I don’t have the patience to do equations with the WordPress menu.
You’re welcome!
I really appreciate this.
Thanks, that’s clear!
I understand how to get the F value and why it is important. When the F statistic is “large” then the between group variation is greater than the within group variation. My question is what is a “large” F value. Is it greater than 1? 2? 10?
Thanks in advance!
This is great, there is one correction, however. When describing the equations for the between groups variance, you say to:
“First, subtract each group mean from the overall mean
Second, multiply by the number in each group”
Yet the equation shows to square the results from the first step. I’m not sure if the steps are right, or the equation is right (though, I’m assuming it’s just an omission by the author). Anywho, this was a great explanation, thank you!
You are correct. It should be squared. Made the correction. Thanks for catching it.
Steph –
An F-value of 1 is VERY low. It says the variance between groups is exactly what you would expect by chance.
I would look at three things, the F-value, the p-value and the r-square. That’s another post. Maybe I should get on that after I check out of this hotel room which I am supposed to do in 45 seconds (not kidding).
is this model is good because F-statistics is low?
No, the model is BAD if the F value is low. It means that the variance explained by the independent variables in the model is low.
Thanks for the clear explanation – it’s so hard to find stats and science methods in laymen’s terms!
Thank you for this! I’m a second year medic trying to write a review on different explanations for the pathophysiology L-dopa induced dyskinesias in Parkinson’s patients, expecting to be looking at means, SDs, ORs, the odd bit of t-test and I^2 as statistical analyses.. then I was confronted with some F statistic!? Your blog broke it down for me in such a way that I can now understand the results, and I might even be brave enough to do a little bit of critique on them now in the essay. Thanks so much!
Please help me understand.How do I interpret these results whereby the
F value=2.595 and the P-value =0.079
Total number of groups=3
Observations=125 (n=125)
I understand that the df will be 2 and 122
I saw this blog the night before my Statistics Exam, and it was godsend. I was relieved to finally make sense of the i,j, x and such abstract stuff.
Thanks
Hi AnnMarie,
Thanks for the explanation of ANOVA. I keep seeing that a low F is bad (closer to chance) but what is low? Are we on a scale of 1-10 or 1-1000 here? If you expected the IV to explain a moderate amount of the variance what kinds of F would you expect to see, 5, 50 or 500?
Thanks
Janine
An F-value is the ratio of two estimates of the variance, an estimate derived from the variance BETWEEN GROUPS is the numerator and an estimate derived from the variance WITHIN GROUPS. An F-value of 1 means that you get the variance between groups that you would expect given the variance in the population – so, an F of 1 is what you would expect by chance. Anything close to 1 is bad. There isn’t an upper estimate but it would be kind of weird to see something where the variance between groups is 1,000 times as high. I’ve seen F-values of 5 to 15 pretty often in studies where the treatment has a major effect.
Who could me help describe on F value for SAS;the result is F=99999.99 and p>f 0.0001.
I would like to know about F meaning as I post. also, R square = 1.00. Cv = 0. who can help me please?
This has really helped me do my descriptive analysis deduction… I’m greatful
I read your first paragraph and got excited. I have pored by textbook and dozens of websites and NONE of them explain how to INTERPRET F test results. Its used to determine if we should assume equal variance or not, great, how do we make that decision? If F=0.5 do we reject equal variance? I need halp.
Thank you. You helped me so much in figuring out ANOVA!!!
Thank you!!
Really helpful, thanks.
Hi,
I have conducted an experiment for my thesis where I have to incorporate Quality by Design (QbD) and have simulated my results using a Design of Experiment (DoE). The software has calculated my results to have an F ratio of about 42, with a probability > F of 0.0227. I have been taught that this ratio is the Signal to Noise ratio, and a high ratio is good because the simulation has used more data than experimental noise under controlled conditions. Is this correct?
Also, what does the probability > F mean in this case?
Kind Regards,
Shah
The probability means there is a 2.27% probability that you would find an F larger than this by chance . I recommend you also look at the R-squared for the percent of variance explained.
Hello I am trying to decipher what the meaning of my data is. I am look at the relationship between troops and regime type. I got an F=.52 and a pvalue of .5922
The means of the regime types are 37, 101.2955, 61.92.
I understand that we should fail to reject the null because it is a large p-value but the F statistic is misleading.
I don’t know why you think the F-statistic is misleading. An F value of 1 means the variance among means is exactly what you would expect given the within-group variance. An F-value of .52 means this is only about half (52%) of the size of a variance you would expect given the variance within groups. In other words, it is highly likely these mean differences occurred by chance – which is also the conclusion you reach given your p-value.
Thanks for explaining a hard-to-understand concept. I get a bit confused what (y subscript i) means in the images. It seems to mean two different things.
In the first sigma notation, y subscript i represents an individual y value.
In the second sigma notation, y subscript i represents a groups’ mean.
I came from this site which linked you
https://stats.stackexchange.com/questions/301959/anovas-f-statistic
Thanks.