Advice on marriage, Euclid & logistic regression

My friend, Gokor Chivichyan, a mixed martial arts instructor, once gave this questionable advice to his students,

“Women usually just say they’re fat to get attention. So, me, I agree with them. If she says she’s fat, I say, yes, you fat but we like you anyway. If she’s really fat, though, you just have to dump her. Not if she’s your wife, though. Then, it’s too bad but you have to keep her anyway and take care of her because she’s the mother of your kids.”

(For the record, I have met Gokor’s wife and she is both lovely and charming.)

We tend to keep our private life extremely private. Dennis has been referred to as “your alleged husband” by my friends, who have never met him.  Recently, another friend of mine, my former business partner from Spirit Lake Consulting was visiting and, after knowing me for 20 years, met my husband for the first time. My friend commented,

“Your husband really loves you.”

I was a bit miffed that he found this so surprising.  I think one reason this is a surprise is that we so often categorize people into single boxes. I was a world-class athlete while my husband hates all exercise. Being a sixth-degree black belt, I once suggested to him that perhaps he could learn judo for exercise. His response was,

I’m not doing anything where people touch me unless I get to have sex with them at the end of it.

As I was laying in bed this morning with my eyes closed, trying to avoid morning, Dennis was carrying on about the Complete Works of Euclid, which proofs were not really proofs, but axioms, the incompatibility of irrational numbers with early Greek geometry, the inefficiency of using geometry for certain proofs rather than algebra or calculus. This is why my husband loves me. Not only did I not find this boring and throw a pillow at him, which most of the women of my acquaintance might have done, but actually opened my eyes, made a comment or two about how it fit exactly with what I was thinking about, which happened to be …

The geometric concept of a line is that it extends infinitely in both directions. What most people think of as a line, with two end points,  is really a line segment. Most of us learned this in high school or middle school and don’t really think about it much. However, sometimes it becomes relevant.

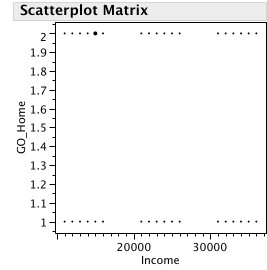
Let’s say you were trying to predict a dichotomous dependent variable. Since it is around Christmas time, let’s pick whether a person is traveling home for the holidays or not, which we have coded 1= no, 2 = yes.  That might be a very useful fact for people to know who were in either the travel or family therapy industries to target their marketing/ determine outpatient clinic hours.

This is a dichotomous variable and you can see that it plots pretty terribly against a continuous predictor variable – say, income.

You can see that the linear equation

Y =  a + bX

is just plain wrong here. It doesn’t fit. Very, very far from the assumption that a line extends infinitely we are stuck with a stupid line that goes from 1 to 2.

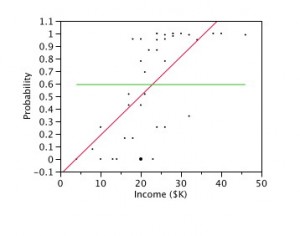
How about probability then? We could use the probability of going home for Christmas by income. That will extend from 0 to 100, which is certainly closer to infinite.

Well, this is better. It sort of approximates a line.In the graph above, you can see the obtained regression equation

Y = -.1236 + .0313X

(I know you were dying to know.)

You can also see the predicted values it gave me for incomes below $5,000 are negative. I guess those are the people who are not coming home even IF hell freezes over. The probabilities for people with incomes over $40,000 are above 1.0.  I guess that means they are going home twice, once to mom’s house and once to dad’s place in the Hamptons with his trophy wife.

So, we have one case, with just the binary outcome, which is clearly not linear. We have another case, predicting the probability of the outcome, which may be linear, but is actually a line segment and not a line. That may be true in theory for lots of things. I doubt income extends from negative infinity to positive infinity, although Bill Gates and Warren Buffet are doing their bit to extend the right side of the distribution for themselves while the Republicans and certain banking and investment firms are making a best effort to extend it on the left for all the rest of us.

There are a whole bunch of reasons that using linear regression is wrong when you have a binary dependent variable, and the fact that it is flat not a linear relationship is just one of those.

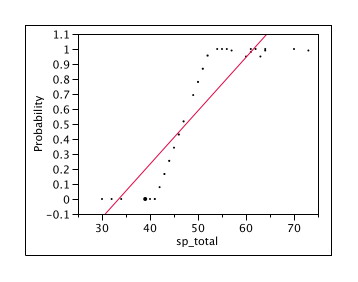
Now, if I were an ancient Greek, I would include a lot of geometric examples, not really proofs. If I were an ancient Greek that had access to JMP 8 software I might include another variable graphed against probability and say, “Looky here”, or however you say that in Greek.

This is a very important point – Greek or not – even though the relationship charted above is very high – R-squared = .78 to be precise, it is clearly not a linear relationship. It is an S-curve and it looks very much like a logistic relationship.

Three very important points emerged from this:

1. The potential to teach kids the basic understanding of some of the more abstract concepts of mathematics by pictures. I can see how you could start with these graphs and do a linear relationship, then log one variable, log both and start to see the different types of pictures. Those Greeks were on to something. Too bad they didn’t have JMP. Never know what they could have achieved. (Click here for link to random JMP page.)
2. The idea of using graphs to teach students is intriguing, and yet I am puzzling how I could drag the world’s most spoiled twelve-year-old away from the Disney channel downstairs and get her to see it that way. The use of graphing calculators in mathematics is not new, but neither does it seem to be particularly effective. This is all fascinating TO ME because I see the end point of making predictions. Perhaps we should spend the first few weeks of mathematics on why what we are about to do is important?
3. I was thinking that I had failed miserably on most of the #reverb10 prompts because, well, frankly, I’m more interested in examining logistic and linear relationships than ruminating on my life. Then, it came to me – what’s the one thing I have come to appreciate in the past year? That I’m married to someone who would wake me up by bringing me coffee in bed and talking about the complete works of Euclid!