Are we living longer – or not?

It is not every day that my refrigerator provides insight into a statistical problem. My daughter gave me this magnet.

BIRTHDAYS ARE GOOD FOR YOU. STATISTICS SHOW THAT PEOPLE WHO HAVE THE MOST BIRTHDAYS LIVE THE LONGEST.

which led to my thoughts on life expectancy using open data. Kaiser Permanente collected data on two cohorts of patients, those who were 65 years old or older in 1971 and in 1980.  After having published some research supported by the National Institute on Aging, on topics of interest to themselves and their funding agency, like cardiovascular disease, the investigators made their data available through ICPSR where I downloaded it.

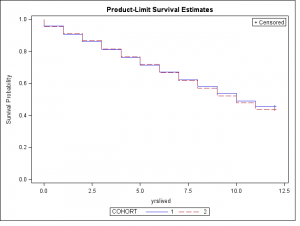
I had read elsewhere that the life expectancy had increased even within that decade. If that is true, I reasoned, looking at the survival curves for people from the 1971 cohort (1) and the 1980 cohort (2) would show some differences.

 

 

 

 

 

 

When I look at the survival curves by strata

(

PROC LIFETEST DATA = saslib.death ;

STRATA cohort ;

TIME yrslived *dthflag(0) ;

)

I get the survival curves above and it is pretty clear they are the same. If anything, it looks like Cohort 2, those born later, actually had a slightly higher mortality near the end of the study.  For those of you who feel uncomfortable just eyeballing the curves, even when they are as close to identical as this, the Log-Rank test  for equality of strata = 1.27 (p > .25).

And yet, on the other hand, when I did a t-test by age, I found that the 1980 cohort did live significantly longer, with those who turned 65 in 1971 having a mean age at death of 84.7 while those who turned 65 in 1980 had a mean age at death of  85.3  (p = .01 ) which leads to the conclusion that people from the 1980 cohort did live longer.

What’s going on here? This is the point where the getting to know your data part that I am always harping on comes into play. Note that Kaiser-Permanente said that they collected data on people who were 65 or older  in 1971 or 1980, not who turned 65.

In fact, the two samples were not the exact same age. The mean age of the 1971 sample was 75.7 and of the 1980 sample 76.1 . So, of that .6 year difference in lifespan, .4 of it existed before the study even started.

What difference would that make? Well, let’s go back up to my refrigerator magnet. What does the fact that someone has lived to 65 tell you? Most unequivocally that they did not die of anything at an age earlier than 65. They weren’t killed in the Vietnam War when they were 19 years old, in a car crash with a drunk driver when there were 33, from colon cancer at 56. Because 100% of the population of people who live to 65 have escaped these hazards for the first 65 years of life, they are NOT representative of the population in terms of life expectancy. This is why when you read articles they have statements like, “For an American male who has lived to age 65, life expectancy is ….”

The qualifying phrase is necessary because those who have had more birthdays already are expected to live longer than the general population.

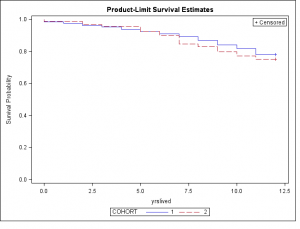
So, I pulled out those who were 65 when the study started and looked at the survival curve

SURVIVAL CURVE FOR PATIENTS AGED 65

COHORT 1 (1971) AND COHORT 2 (1980)

A t-test of years lived for those in Cohort 1 versus Cohort 2 using only the 290 subjects who were 65 years old at the start of the study produced a very non-significant t-value of .56 (p > .50) .

T-tests for subjects at age 75 and age 85 produced similar results.  So, based on these data, the answer to the question of at least whether patients of Kaiser Permanente have increased in life expectancy over the 1970s is, “No”. This isn’t a comment on Kaiser Permanente one way or the other, merely an observation that it is unlikely that their patients are completely representative of the population.
Just an aside, a million points to people who put their data on the web and open to all comers. This shows two traits I admire. The first is generosity, allowing someone else to benefit from your efforts in collecting the data, with no expectation of return. The second is courage. It takes a good amount of courage to publish your results and then make your data available so anyone who wants can re-analyze the data and perhaps come up with a competing conclusion. So, props to you.

P.S. You can buy the hand soaps on etsy. I have no affiliation with them, I just thought they were funny.