(Or: Why a computer will not be replacing me any time soon)

[Originally, the second half of this was supposed to be an explanation of the real use of multiple imputation which is in estimating parameters but then my daughter came to pick me up early and I got the flu so I am now finishing the second half as a separate post and pouting that John Johnson  goes on Santa’s nice list for saying it faster and shorter than me. However, since I was in the middle of writing it, I am going to do it as the next post anyway!]

I am a little hesitant to do multiple imputations or really substitutions for missing data of any type. I go through life with the “call a spade a spade” philosophy and what we are doing here is making up data where none exists. However, there is a difference in the quality of data one can make up. For example, if I asked my little granddaughter,

“What is your best estimate of the average number of clients the Arcadia branch served on Tuesday, January 19th, 2003?”

Her most likely estimate would be,

“Elmo!”

If I put the same into SAS (or SPSS)  it would be the equivalent of asking, since I do, contrary to appearances, know what I am doing,

“Given that the 19th was a Tuesday, in the first quarter of the year and we have data on the Arcadia branch for every other day in January and for the last seven years, they are in an urban area over 3 million in population, what’s the best estimate of the number they served?”

If I were to do this, I would include something like:

PROC MI DATA= in.banks OUT = banksmi  ;

VAR qtr weekday urban branch customer ;

I might still get an answer that makes only a little more sense than , “Elmo!”, say  -5 or 146.783 . Well, I really doubt that negative five customers came to the bank that day. What would a negative number of customers, be, anyway, bank robbers who withdrew money they did not put in?

You need to apply some constraints, which PROC MI lets you do. Here is an example of something I actually did today:

PROC MI DATA = fix2 OUT =fixmi MINIMUM = 0 ROUND = 1 .01 .01 .01 1 1 1 1 1 ;
VAR ACD_Calls A_speed A_time ab_time aban_calls qtr t_day year weekday skill_name ;

The MINIMUM = sets the minimum for all variables to be zero, since we can’t have a negative number of callers and negative time is one of those concepts that was probably covered in philosophy and other types of courses I did my best to weasel out of through one undergraduate and three graduate programs. The ROUND = sets the number of callers to be rounded to 1, the time for speed of answering and length of call and the time people wait before hanging up (less than 11 seconds) to be rounded to .01 and everything else to be rounded to 1.

SPSS also offers multiple imputation as part of its missing values add-on. If you have it installed, you select from the Analyze menu Multiple Imputation and then Impute Missing Data Values.  At this point a window pops up letting you select the variables and giving you the option to writing the output to a new dataset.

You can also click on the Constraints tab at the top and another window pops up which allows you to set constraints such as a minimum, maximum and rounding.

All of the stuff you can do with windows and the pointing and clicking you can do with SPSS syntax also but I have found that most people prefer to use SPSS precisely because they DON’T want to do the syntax business. [Note that I said “most” so if you are one of those other people there is no point in being snippy about it just because you are in the minority. Try being a Latina grandmother statistician for a while and you’ll know what a minority feels like.]

Well, how well does multiple imputation do? Here is a really extreme test. I calculated the actual statistics for the month of October and then deleted about half of the month’s data for every group.

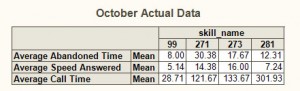
Below are the initial statistics with half of the values imputed:

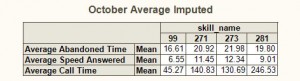
Okay, well normally you need something more extreme than multiple  imputation if  half your data are missing, like a new project, but this isn’t terrible. You might notice that the least error is in the last column. Why? Well, it turns out that this is the only department that is open on weekends. The others had data imputed for Saturday and Sunday but were never actually open on those days.

I could have done something more sophisticated but since one of my daughters borrowed the car and was downstairs waiting to pick me up, I greatly decreased the error from the actual data by one simple change:

in the imputed dataset, I added the statement

IF skill_name in(99,271,273) and weekday in (1,7) then delete ;

This deleted those records that had data for days the department was not open and increased the accuracy of the final dataset substantially. Here is the take away lesson – the SPSS people with the decision trees and the knowing what variables to constrain, they are on to something. You can do all of that in SAS also, but when you attend events like the SPSS Directions conference , that is their real emphasis, where at places like SAS conferences (more statistically-oriented) the emphasis is more on setting constraints and doing the actual procedures. What you want is both of those things, the former of which includes considerable expertise in the area you are analyzing, be it IQ scores, glucose levels or average number of hamburgers served, and the latter assumes some knowledge of statistics. If you add in a good ability to code, you might actually have a better answer in the end than

Elmo!

Now I am going to go downstairs and hope my daughter has not crashed my car into the lobby and run over the guard at the front desk. Wish me luck.