Probability Rules: Why the house always wins

Let’s say that all you knew about probability were some basic rules. Would it be enough to convince you that gambling is a bad bet? I think so.  Let’s begin with these four:

Probability of something not happening = 1 – the probability of that something happening

P(Not X) = 1 – P(X)

Since the total of all probabilities = 100%  , that is, there will be SOME result, and the probabilities of something not happening and the same something not happening are mutually exclusive, the probability of something NOT happening must be 100% minus the probability of it happening. (This relates to the next rule).

The probability of either of two mutually exclusive events is the sum of their individual probabilities

P(A or B) = P(A) + P(B)

Notice that the key phrase there is mutually exclusive. Here is where people often go astray.

There was the famous case of the gambler who bet that a six would come up at least once in four throws of a die. A person misapplying this rule would say the probability is

2/3 or 4/6 that this would happen.

That is, your odds are 1 out of 6 possibilities on the first throw, the second throw, the third throw and the fourth throw.

These are not mutually exclusive probabilities. A person can throw a six the first time and the third time. So, no, this rule won’t work.

For independent events, the probability of any combination of them is the product of the individual probabilities.

That is,

P( A and B) = P(A) * P(B)

Let’s take our gambler again, written about in a free and highly recommended book on probability by Grinstead and Snell.

So, the probability of NOT getting a six is 5/6 – since there are 5 sides on a die that are NOT a 6.

The probability of not getting a 6 four times in a row is

5/6 * 5/6 * 5/6 * 5/6  = .482

Since  48.2% of the time you won’t get a 6, that means 51.8% of the time you will. The odds are in your favor to bet on getting a 6.

So … why did the gambler lose money? This, my friends, brings into consideration,

The Law of Large Numbers

The best description of the Law of Large Numbers I have read comes from wikipedia

“It follows from the law of large numbers that the empirical probability of success in a series of Bernoulli trials will converge to the theoretical probability.”

A Bernoulli trial is an event that can have one of two possible outcomes, and which outcome is obtained is determined at random. Sounds like throwing a die and getting either a 6 or not a 6.

So, over the long run, the larger and larger number of trials you have, the closer you will get to the theoretical distribution, in this case, getting a six 48.2% of the time.

Incidentally, for all the trashing academics do of wikipedia, I have found their sections on statistics to be extremely accurate and well-written. Whoever the people are who write it, kudos to them.

So, if we had an infinite number of trials, we would always end up with 51.8% of the time a 6 coming up on four throws of a die.

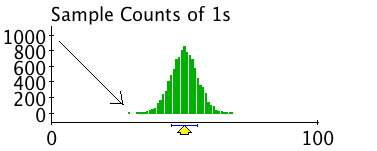
Here are the results from someone who bet 100 times on a binary outcome, with a distribution of 10,000 trials. That is, assume you went to Las Vegas for 10,000 days in a row and every day you made 100 bets.

Two take-away points:

1. The house always wins because the casino makes a LARGE number of bets. If you count every time someone pulls a slot machine or bets on 21, it is hundreds of thousands of bets a day. If they are taking the equivalent of that 51.2% bet, over a large number of trials, they will always win. If the odds are 50%, as above, they are going to be centered around 50. If, as on most bets people make, the odds are more around 52% , in the house’s favor, the distribution is going to be centered around 52%. More than half of the time, the house wins.
2. People will say things like, “Yes, but what if you are the one on the end before the house starts to win? What if you are that one person out of the 10,000 where the die comes up with a 6 only 30 times out of 100? You’d win big, wouldn’t you? That’s possible, isn’t it? Yes, it is possible, but it’s not the way to bet. The odds are not zero, but they ARE against you.

So, you now you know why statisticians are no fun in Vegas. In fact, I was at a conference not long ago where someone at the casino told me,

“We hate you people (statisticians). Everyone always makes less money on the statistics conferences than any other event because they understand the odds, so they very seldom gamble.”