When acceptance is really rejection: Death by Green Pants
The model is non-significant, therefore my theory is supported.
Huh?
Just when you thought it was safe to get back into statistics… It took you two years of graduate school but now you have it down. P-value low = good, relationship detected, publication, tenure, Abercrombie & Fitch models at your feet.
P-value = high, no relationship, no publications, no money, dating the creepy guy next door.
Enter Hosmer to screw things up.
There are a whole bunch of reasons you might want to do a logistic regression (no, I’m serious). If you want to predict a categorical dependent variable like death, drop-out or watching Afghan Star. If you were going to do a propensity score match you would start with logistic regression. If you plain can’t think of anything else to do with your evenings.
The first thing would be to see if your dependent had a relationship with your grouping variable or you really are wasting your time. Okay, now that is settled, you have found that people seen in hospitals with Intensive Care Units are more likely to die than those seen at other hospitals.
You also want to see if the variables on which they differ have anything to do with the outcome. For example, I ran an analysis where I coded their favorite colors of pants – blue, brown, white, black or green pants (seriously, who buys green pants?) . People who went into intensive care were more likely to own green pants. To test if this is significant, I run a logistic regression with death as the outcome variable and pants color as the predictor.
In SPSS you go to ANALYZE > REGRESSION > BINARY LOGISTIC
So, the Hosmer and Lemeshow Test is statistically significant with a chi-square of 349.06, df = 4 and p < .001. Is that exciting? Do I immediately publish an article on “The American Apparel Effect” and how poor fashion taste is dangerous to your health?
Not so fast. You see, Hosmer & Lemeshow tests the Goodness of Fit of the model predictions to the observed data. If you reject the hypothesis that your model fits the data, that is bad!
In my next logistic regression, I used age over 65 as a dichotomous variable. My second variable was the Dr. MechOth scale. Dr MechOth (not her real name) was a friend of mine when I was a young Assistant Professor who occasionally hung out in bars. Dr. MechOth rated all men on a 1 to 3 scale, where 1= “Yes” , 2 =”Maybe if I was drunk” & 3=”I couldn’t get drunk enough”.
The results of the Hosmer & Lemeshow test shown below, with a chi-square = 4.52, df = 3, p > .20 show that the data fit the model somewhat, although it could be better.
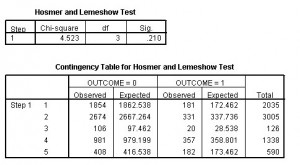
Does this mean that in logistic regression high p-values are always a good thing? Nope, that would be too easy for you to remember. In fact, no sooner have we inverted our understanding of p-values but now it is time to do it again. When interpreting the COEFFICIENTS, a low p-value is a good thing. So, which of Dr. MechOth’s groups one is in, and being really, really old are related to probability of death.
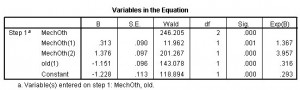
Sadly, my original hypothesis about death by green pants is not supported and all I have discovered is that if you are really, really old and no one would go home from a bar with you if you are the last person on earth, you are more likely to keel over dead from natural causes or suicide, whichever comes first, than hot, young people.
I do not think I will be winning the Nobel Prize for Medicine any time soon. I wonder if that guy next door likes Cup-A-Noodle soup.
Which is cause and which is effect is still a tough call even after finding a great corelation.
Or even IF there is a cause and effect. If (pulled out of thin air) 97% of traffic accident victims had eaten a pickle the week before would that tell you anything? Of course it might tell it was summertime but that is about it.
PS Statistically speaking: half of all brain surgeons are below average in skill & competence!!!