Why chi-square is expecting the expected value
This is one of those things that is obvious after someone points it out to you and you smack your head saying, “Of course! I knew that.”
As I was going through everything I have to say about analyzing categorical data trying to winnow it down to a three-hour workshop for the WUSS conference (Western Users of SAS Software) next week, I wondered how many people ever THOUGHT about probability again once they had finished that chapter or two in their statistics course.
Professors are optimistic when they believe that students forget almost everything they have learned six months after the course. I have found that if you give chapter tests, students forget a lot of what they have learned by the next week. And I don’t blame them. Very seldom have I seen a real effort made in textbooks to draw connections back to what was learned previously. This is why I have a hatred, varying only in degree of venom, for all mathematics textbooks ever written.
So, as a public service, here is what the information you learned about probabilities has to do with expected value.
The probability of two independent events occurring is the product of their individual probabilities. That is, under the assumption that
the probability of event A occurring – P(A)
— is unrelated to
the probability of event B occurring – P(B)
— then the probability of A and B occurring , which is written as P(A U B) and read as “the probability of the union of A and B)
is equal to P(A) * P(B)
Let’s say that whether or not you have your own desk at home (yes or no) as a middle school student is unrelated to gender. Parents are equally likely to provide a desk for a boy or a girl.
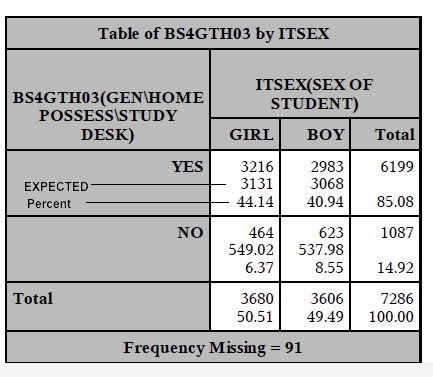
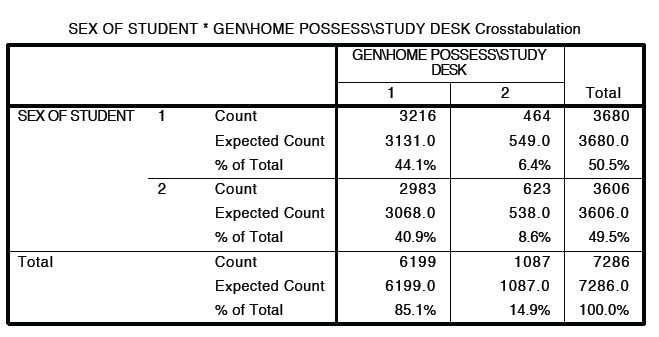
Let’s say we have a population of 7,286 eighth-graders that is almost exactly divided between girls (50.51%) and boys (49.49%).
We also find that
of those 7,286 eighth-graders, 85.08% have their own desk.
Then our EXPECTED frequency for girls having their own desk is 50.51% times 85.08% times 7,286
.5051 * .8508 * 7286 = 3,131
What an amazing coincidence, that is exactly what the expected frequency is in this table.
If you remember (and if you never knew, let it be a brand new surprise to you) that the chi-square is calculated by the sum of the observed minus the expected squared (hence the name chi-square) divided by the expected
So, the further your observed frequency is from the frequency expected under the assumption the two variables are independent, the larger your chi-square value.
Why divide by the expected? Well, if your expected value is 10 and your observed value is 20 then 10 more than expected is a lot of difference, it is twice what was expected. On the other hand if your expected value is 2,000 and your observed value is 2,010 then your observed is actually pretty close to the expected, percentage-wise
How to get some tables….
I was feeling all pointy and clicky today so I produced the SAS table above using SAS Enterprise Guide. Go to the TASKS menu, select DESCRIBE and TABLE ANALYSIS. Under cells be sure to click on expected frequency and cell percentages. (If you are using a screen reader, click here for an html version of the table)
If you want to do the same thing in SPSS you can use this syntax
CROSSTABS
/TABLES=ITSEX BY BS4GTH03
/FORMAT=AVALUE TABLES
/STATISTICS=CHISQ
/CELLS=COUNT EXPECTED TOTAL
/COUNT ROUND CELL.
Or, you can go to ANALYZE then DESCRIPTIVE STATISTICS then CROSSTABS then click on CELLS and click the button next to expected.
And now I was feeling guilty because even though we have four desks in the house, two are in my office, one is upstairs and one is in the living room so that anyone who wants to work on the computer while watching TV can. None of them belong to the world’s most spoiled 13-year-old personally.
But .. then I re-read the question and saw that it just asked if there was a study desk or table the student could use. So, we are off the hook. Which is a good thing, too, because her shopping list for today includes:
One Halloween costume
Zero Desk
All of the make-up sold by MAC and Sephora
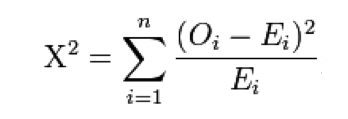
I love this article, well done!
Just a clarification “then the probability of A and B occurring , which is written as P(A U B) and read as “the probability of the union of A and B)
This should be P(A n B) probability of A intersection B.